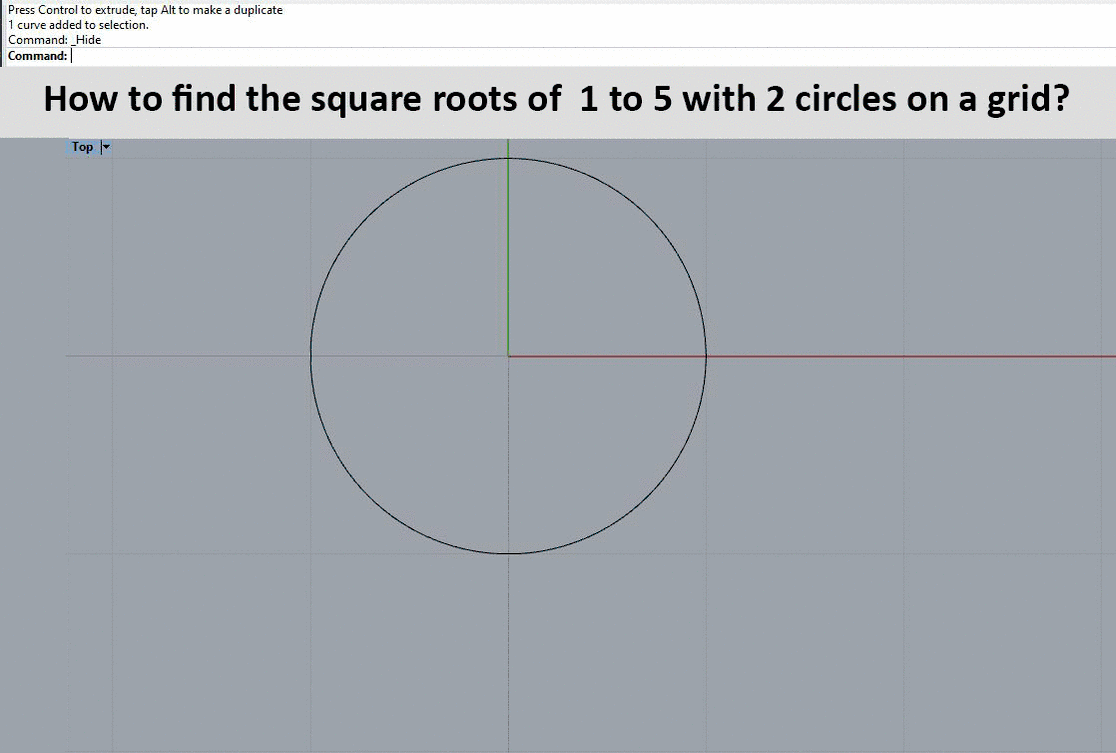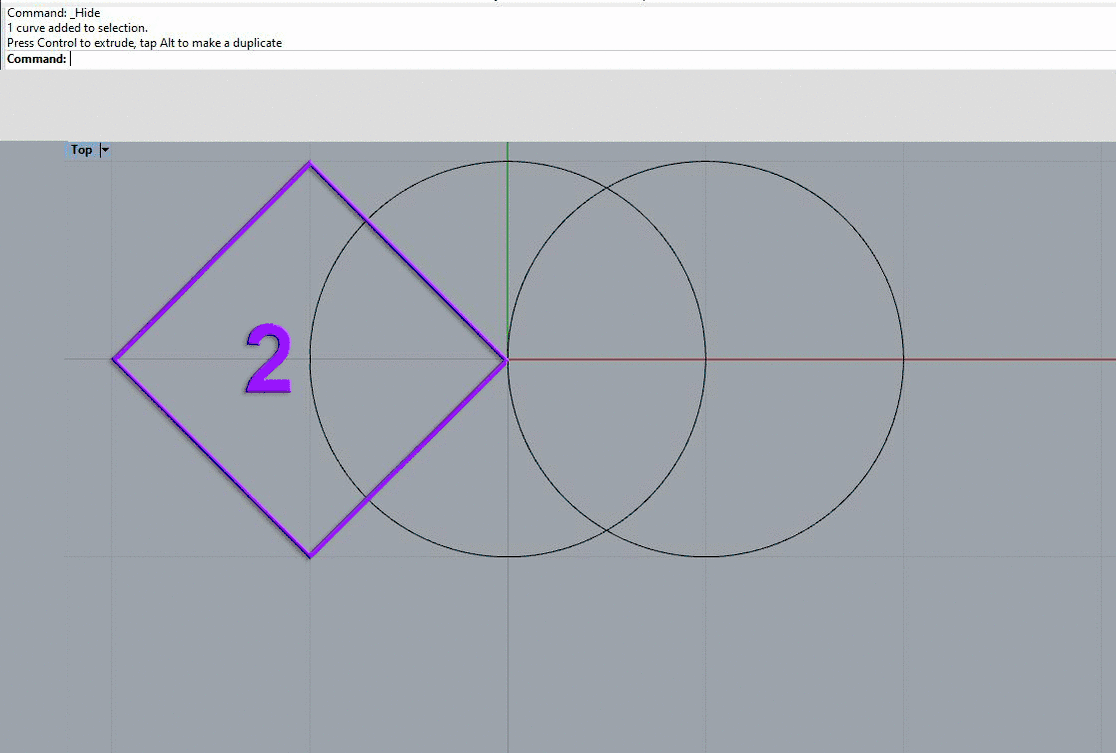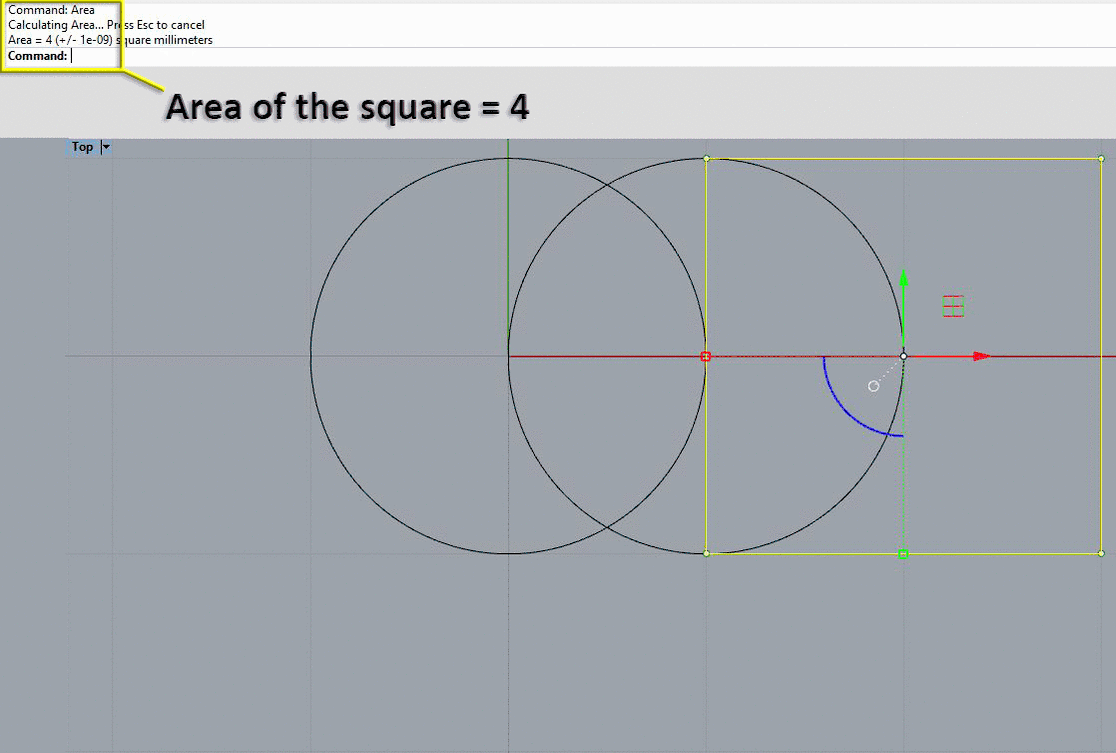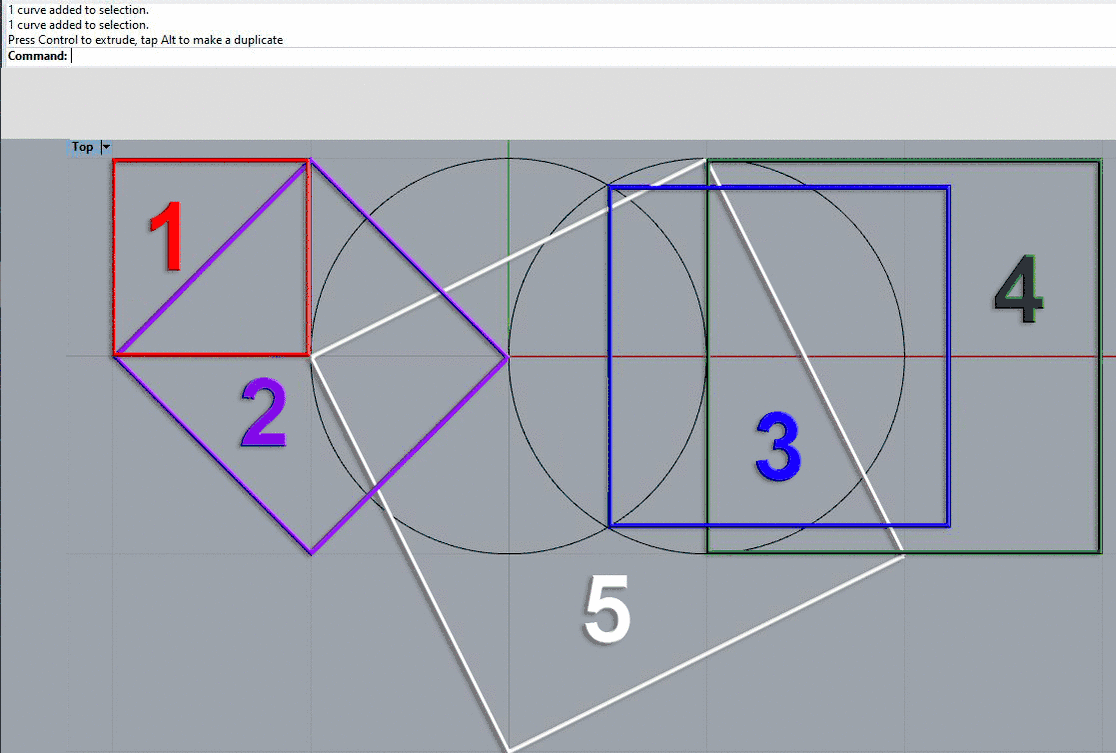
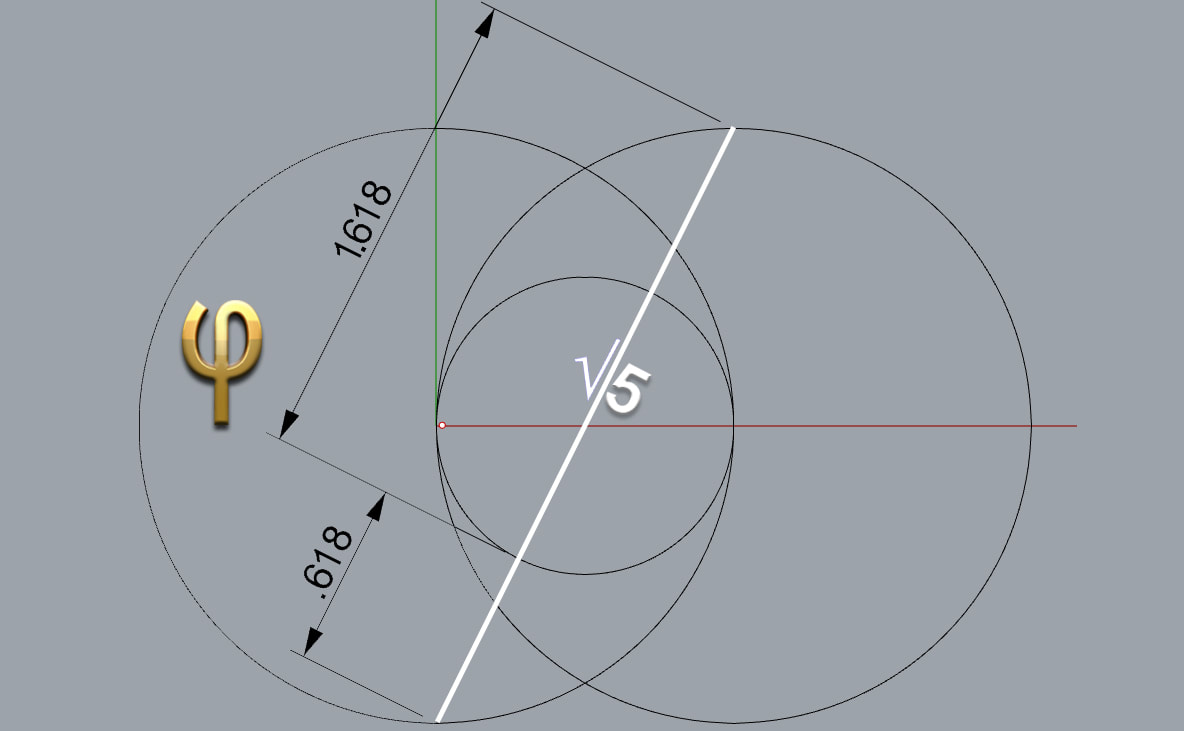
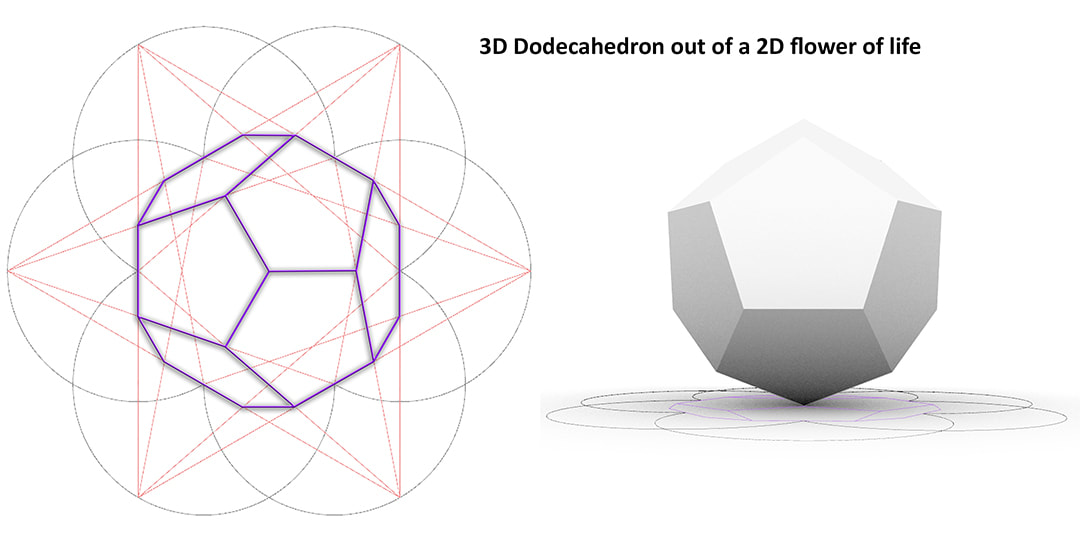
With the mathmagic relation between geometry and numbers we can find the square roots of 1 to 5 with only 2 circles!
Finding Phi with Vesica Piscis
There is a lot of ways to find Phi in Geometry:
www.cut-the-knot.org/do_you_know/GoldenRatio.shtml
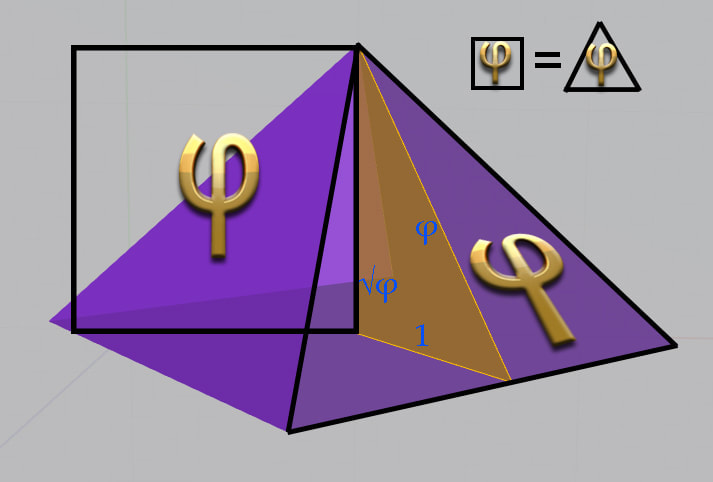
Relation between 2 and 3 dimensions
|
.5236 π/6 and also the ratio of a sphere whose diametre is equal to the side of a cube.
2d became 3d... this number is also in perfect relation with Phi, because 5/6π= square of Phi The perimeter of a triangle rectangle base 2 heigth 1 is 5.236. Curiously the egyptian royal cubit is 52.36 cm. About Egyptians, accordingly to Herodotus the squared height of the great pyramid is the same area as one of its triangle. The only solution to get this result is to construct a Phiramid. You will have no choice but to use a Kepler triangle. This prodigious triangle is 1, square root of phi and phi. Mathemagical relation between 2D of the Kepler triangle and the 3D of the Phiramid. |
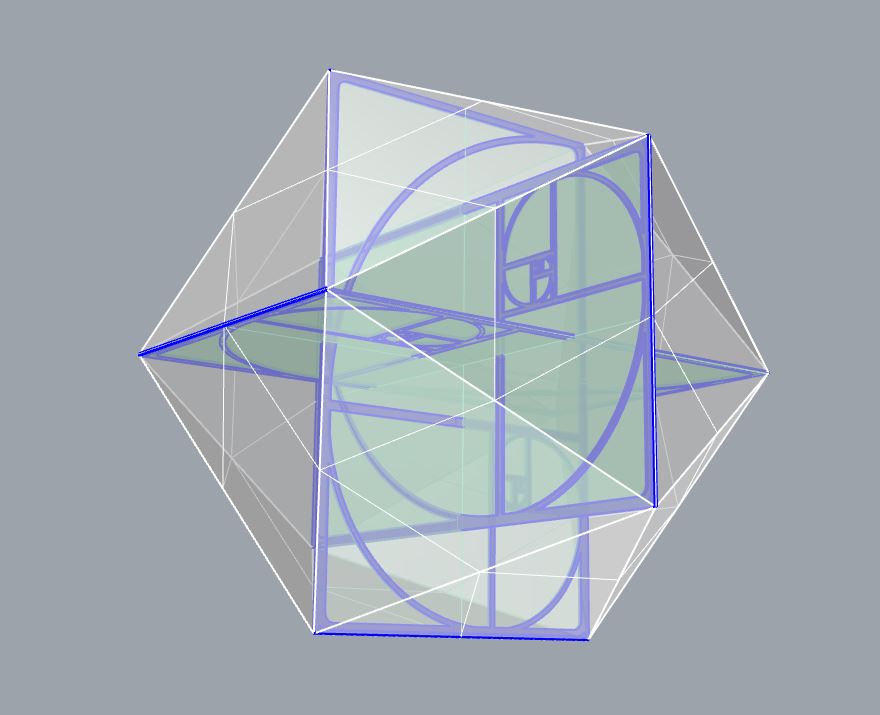
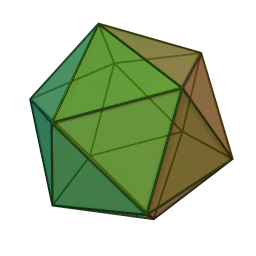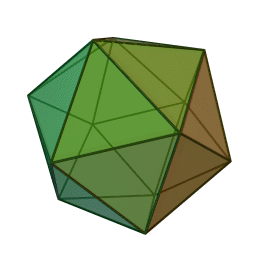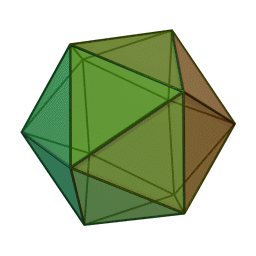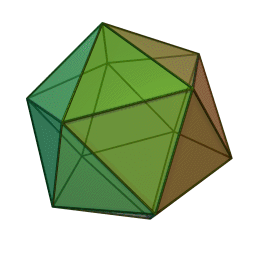
3D Icosahedro based on 3 golden rectangles (2D)
Relation between Phi and Pi
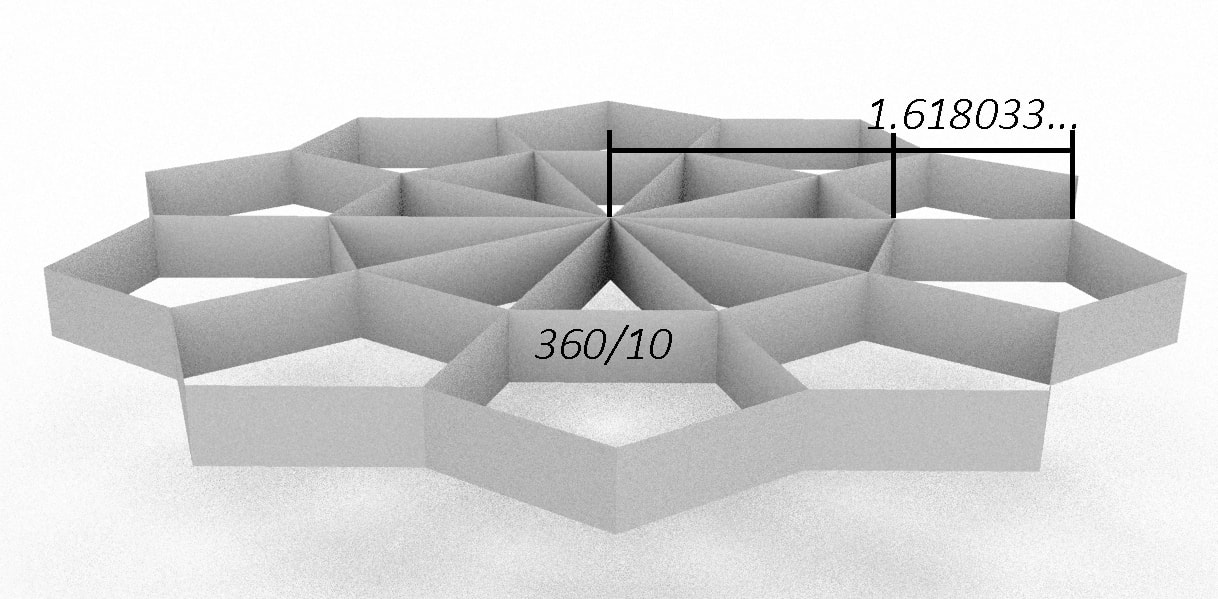
Another perfect relation between Pi and Phi is when you divide a circle by 10, you get 10 golden triangles, consequently 10 regular pentagons
|
The mathematical beauty of this crown of pentagons is that it is constructed on a decagon. There are no other combinations of poligons possible to obtain this result. This is one of the magic of the golden ratio.
Take a look at some other example of golden ratios. www.joedubs.com/the-divine-proportion-golden-phinomena-of-nature/ |
Platonic solid
A Platonic solid is a polyhedron constructed by regular polygonal faces with the same number of faces meeting at each vertex. Five solids meet those criteria: