Music and numbers, Pythagorean Mathemusics
|
Pythagoras was the one who connected the numbers with music, he showed that the harmony of two sounds played together simultaneously, could be explained mathematically. It is said that this brilliant idea came to his mind when he heard some harmonious and disharmonious sounds coming from a blacksmith hammers.
|
Relation between notes and numbers
A sound is a vibration of air that is defined by its amplitude (strong or weak) and its "frequency" or number of vibrations per second (high and low). The ratio of 2 to 1 (a plucked string against the handle in the middle, for example) will sound the most harmonious. This is what is called in music the octave, the sounds, one octave apart between them, are so harmonious that their notes are called with the same name, although their frequency may double several times. That is why it took only seven names for the notes: do re mi fa sol la si or C D E F G A B. After 2/1 found 3/2 and then 4/3. So there is a direct relationship between the musical Beauty and the numbers that can be called the mathemagic mathemusic. |
Notes X 2
When you double the frequency of a note, something very interesting happens, the frequency doubled seems the same sound as the original note, but higher, while each other sound quite differently.
When you double the frequency of a note, something very interesting happens, the frequency doubled seems the same sound as the original note, but higher, while each other sound quite differently.
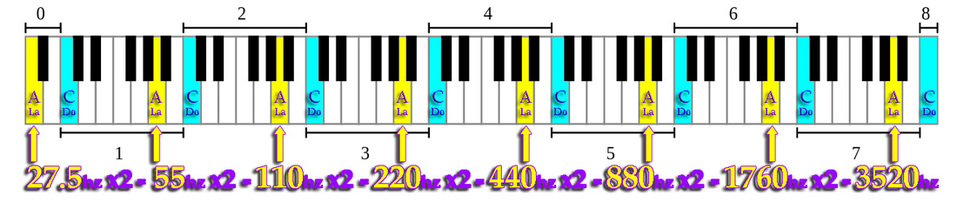
 Based on this Fork A440, frequencies are not integers
Based on this Fork A440, frequencies are not integers
In music, an octave (Latin Octavus: eighth) is the interval between one musical pitch and another whose frequency is doubled.
Scale based on 440Hz
Since the 20th century, most of the forks have a 440Hz frequency reference. This choice gives a frequency scale (Hz) which is not composed of whole numbers, for example:
220
233.082
246.942
261.626
277.183
293.665
311.127
329.628
349.228
369.994
391.995
415.305
440
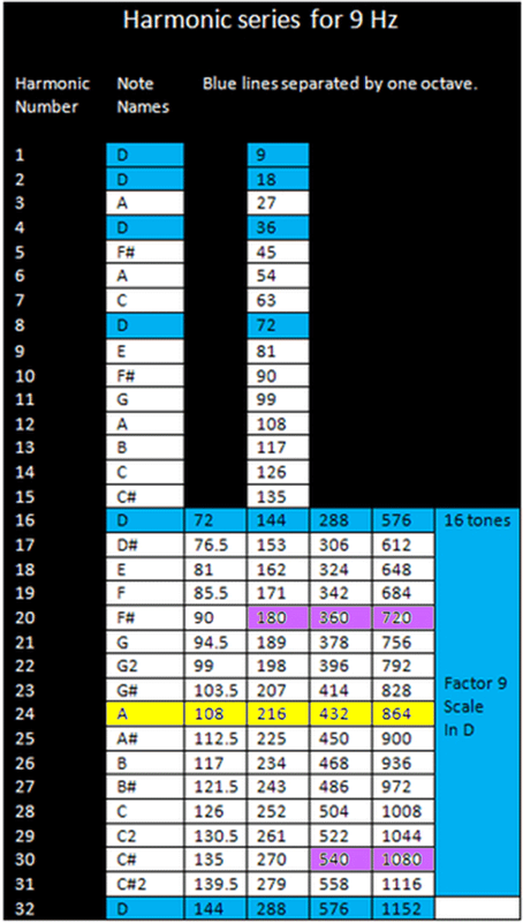
Scale based on 432Hz
We find much more beautiful symmetries in the numbers if we use the former more traditional system based on 432Hz. It become possible to imagine a scale which exploits mathMagics properties of the number 9 as seen in the following harmonic series to 9 Hz
Scale based on 440Hz
Since the 20th century, most of the forks have a 440Hz frequency reference. This choice gives a frequency scale (Hz) which is not composed of whole numbers, for example:
220
233.082
246.942
261.626
277.183
293.665
311.127
329.628
349.228
369.994
391.995
415.305
440
Scale based on 432Hz
We find much more beautiful symmetries in the numbers if we use the former more traditional system based on 432Hz. It become possible to imagine a scale which exploits mathMagics properties of the number 9 as seen in the following harmonic series to 9 Hz
Regular polygons and integers
This scale is not only interesting because it is mostly composed of integers, but also because we find in it numbers like 180 360 540 720 900 1080, which are the sums of the angles of the regulars polygons: Triangle, square, circle, pentagon, hexagon, heptagon and octogon. This coincidence is linked with the mathmagic property of the number 9 and the system 360 as you can see in this video
This scale is not only interesting because it is mostly composed of integers, but also because we find in it numbers like 180 360 540 720 900 1080, which are the sums of the angles of the regulars polygons: Triangle, square, circle, pentagon, hexagon, heptagon and octogon. This coincidence is linked with the mathmagic property of the number 9 and the system 360 as you can see in this video
There is something about 9This video shows the mathmagics properties of the number 9 in relation with the angles based on the 360 degrees system
|

Nine is such an interesting number. The result of all its multiples gives always a digital root of 9:
9x2=18, 1+8=9; 9x3=27, 2+7=9... and so on for all eternity. That is not all, It works also when you divide it by 2,4,8,16,32... 9/2=4.5, 4+5=9; 9/4=2.25 2+2+5=9; 9/8=1.125, 1+1+2+5=9... and so on for all eternity That is not all, all the sums of the angles of all the regular polygons are multiples of 9 and gives a digital root of 9. That is not all, divide the degrees of the circle by 2 and again by 2 and again by 2, forever you will have a digital root of 9. Give a look to this video, it is amazing. The multiples of 9 are numbers comparable to the golden ratio because of their universality. |
Cymatics: visual geometry of sound
|
|
|
|
Destructive frequencies
|
We have seen in the cymatics examples that the music is creative, it shapes matter. It can also destroy it, like in the well-known glass destroyed by a high frequency. This phenomenon is called resonance. An explanation of an expert after the last earthquake in Italy was interesting. He explained that because of the resonance phenomenon the destructive power was greater if the frequency of the earthquake was in harmony with that of the building. This means that a small vibration, if it is in harmony with the building, can have a hugest impact on a stronger building. There is a well-known example by engineers, only the wind vibration was able to destroy the Tacoma Bridge. Another one, the Angers Bridge, was destroyed by the vibration created by the measured steps of the infantry.
|